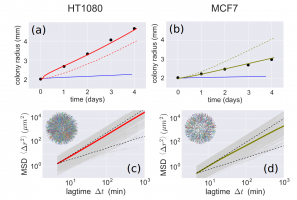
The growth of cell colonies is determined by the migration and proliferation of the individual
cells. This is often modeled with the Fisher–Kolmogorov (FK) equation, which assumes that
cells diffuse independently from each other, but stop to proliferate when their density reaches
a critial limit. However, when using measured, cell-line specific parameters, we find that
the FK equation drastically underestimates the experimentally observed increase of colony
radius with time. Moreover, cells in real colonies migrate radially outward with superdiffusive
trajectories, in contrast to the assumption of random diffusion. We demonstrate that both
dicrepancies can be resolved by assuming that cells in dense colonies are driven apart by
repulsive, pressure-like forces. Using this model of proliferating repelling particles, we find
that colony growth exhibits different dynamical regimes, depending on the ratio between a
pressure-related equilibrium cell density and the critial density of proliferation arrest.
Read the full article in Journal of Physics D: Applied Physics.